- Combinatorics 4
- Constraint 4
- Contact 3
- Simulation 3
- Adaptive Rigidification 2
- Approximations 2
- Finite Element 2
- Stochastic Optimization 2
- Traveling Salesman Problem 2
- Adaptivity 1
- Collisions 1
- Multigrid 1
- Physics-based 1
- Real-time 1
- Rigid Bodies 1
- Rigidification 1
- Shells 1
- Signed Distance Field 1
- Soft Bodies 1
- XPBD 1
Combinatorics
Ordonnancement de tâches sous contraintes sur des métiers à tisser

Generate schedules for looms using fancy methods.
The CONFIDENCE Constraint: A Step Towards Stochastic CP Solvers

Efficiently filter risky solutions with our chance constraint.
Leveraging Constraint Scheduling: A Case Study to the Textile Industry

Warmstart your solve with a faster TSP solution.
Multi-Resource Scheduling with Setup Times: An Application Case to the Textile Industry
Workshop on loom scheduling.
Constraint
Ordonnancement de tâches sous contraintes sur des métiers à tisser

Generate schedules for looms using fancy methods.
The CONFIDENCE Constraint: A Step Towards Stochastic CP Solvers

Efficiently filter risky solutions with our chance constraint.
Leveraging Constraint Scheduling: A Case Study to the Textile Industry

Warmstart your solve with a faster TSP solution.
Multi-Resource Scheduling with Setup Times: An Application Case to the Textile Industry
Workshop on loom scheduling.
Contact
A Multi-Layer Solver for XPBD

Want rigidification without the drawbacks of adaptivity? Use this multigrid-like solver.
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Adaptive Rigidification of Elastic Solids
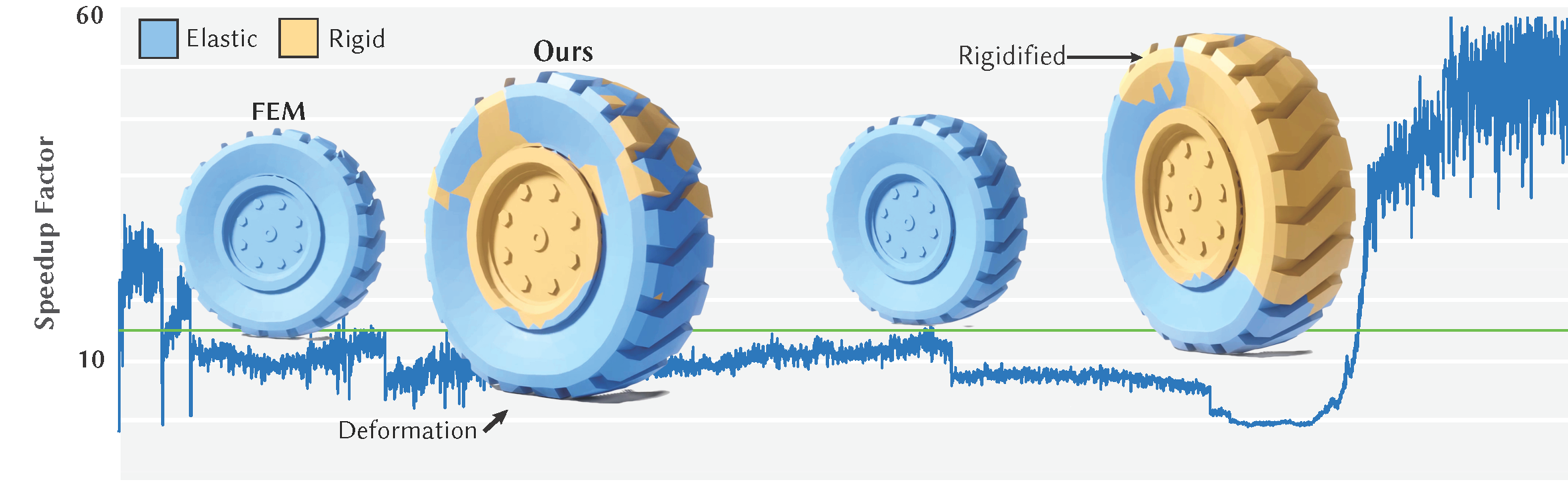
Why waste resources computing deformation on non-deforming regions? Use our method instead.
Simulation
Adaptive Methods for Elastic Deformation

Really just a big passion project of mine.
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Adaptive Rigidification of Elastic Solids

Why waste resources computing deformation on non-deforming regions? Use our method instead.
Adaptive Rigidification
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Adaptive Rigidification of Elastic Solids

Why waste resources computing deformation on non-deforming regions? Use our method instead.
Approximations
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Adaptive Rigidification of Elastic Solids

Why waste resources computing deformation on non-deforming regions? Use our method instead.
Finite Element
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Adaptive Rigidification of Elastic Solids

Why waste resources computing deformation on non-deforming regions? Use our method instead.
Stochastic Optimization
Ordonnancement de tâches sous contraintes sur des métiers à tisser

Generate schedules for looms using fancy methods.
The CONFIDENCE Constraint: A Step Towards Stochastic CP Solvers

Efficiently filter risky solutions with our chance constraint.
Traveling Salesman Problem
Leveraging Constraint Scheduling: A Case Study to the Textile Industry

Warmstart your solve with a faster TSP solution.
Multi-Resource Scheduling with Setup Times: An Application Case to the Textile Industry
Workshop on loom scheduling.
Adaptivity
Adaptive Methods for Elastic Deformation

Really just a big passion project of mine.
Collisions
Real-Time Triangle-SDF Continuous Collision Detection
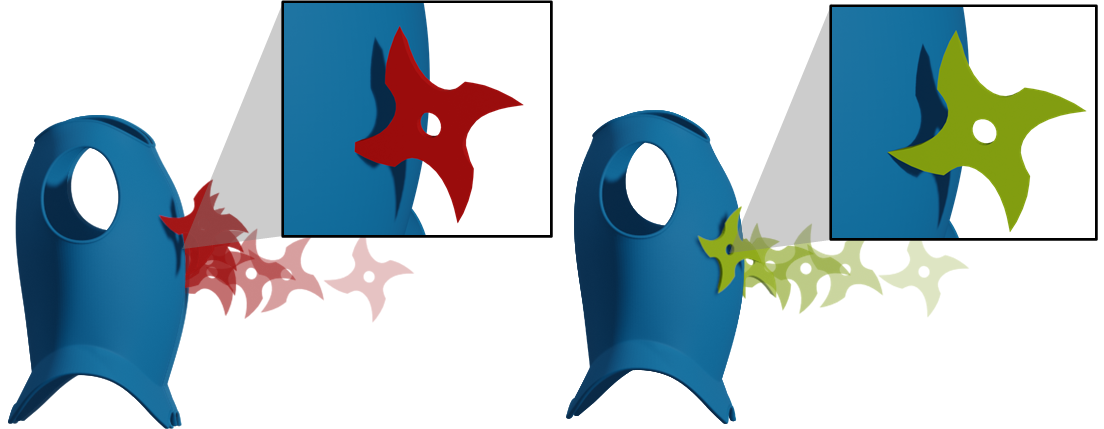
Real-Time Tri-SDF CCD? See how the we made this all possible in this paper.
Multigrid
A Multi-Layer Solver for XPBD

Want rigidification without the drawbacks of adaptivity? Use this multigrid-like solver.
Physics-based
Real-Time Triangle-SDF Continuous Collision Detection

Real-Time Tri-SDF CCD? See how the we made this all possible in this paper.
Real-time
Real-Time Triangle-SDF Continuous Collision Detection

Real-Time Tri-SDF CCD? See how the we made this all possible in this paper.
Rigid Bodies
A Multi-Layer Solver for XPBD

Want rigidification without the drawbacks of adaptivity? Use this multigrid-like solver.
Rigidification
Adaptive Methods for Elastic Deformation

Really just a big passion project of mine.
Shells
Adaptive Rigidification of Discrete Shells

Methods like remeshing target mostly flat regions of shells. We excel at coarsening curves.
Signed Distance Field
Real-Time Triangle-SDF Continuous Collision Detection

Real-Time Tri-SDF CCD? See how the we made this all possible in this paper.
Soft Bodies
A Multi-Layer Solver for XPBD

Want rigidification without the drawbacks of adaptivity? Use this multigrid-like solver.
XPBD
A Multi-Layer Solver for XPBD

Want rigidification without the drawbacks of adaptivity? Use this multigrid-like solver.